The Kelly Formula, a mathematical approach to position sizing

a short essay, by Riccardo Formenti

10/29/2020

Read in your browser

One of the most important, and unfortunately most overlooked, topic in finance is position sizing.

A well devised money management system to optimise your position sizing reduces risks while increasing returns.

But the harsh truth is that investors usually spend hours and hours analysing business fundamentals, macro-economic trends, industry prospects, and everything that will affect a certain company in the future, and then, after arriving to a conclusion, they’ll arbitrarily say: “OK, I like this company, let’s put 5% of my portfolio in it”.

I’m not any better. For months I used the same approach, sizing my positions based on how I felt on a certain security.

But feelings do not belong to investing.

One day I stumbled upon a YouTube video released by hedge fund manager Patrick Boyle (by the way, go check it out, his content is just amazing). He introduced me to the so called Fortune’s Formula. I found it interesting. I started studying the topic.

If you’re interested in the full bibliography used for this write-up, scroll to the end.

The Fortune’s Formula (better known as Kelly formula or Kelly criterion), was discovered in the mid 50s by John Kelly Jr., a Bell Labs mathematician. Initially intended for professional gamblers, the goal of this formula is to calculate the optimal percentage of the total bankroll to wager on a bet to achieve the maximum terminal wealth, knowing probabilities and odds of this bet, and assuming that this bet can be repeated over and over again, an unlimited number times.

In other words, this formula allows to optimise (and maximise) for the geometric mean of returns, better known to finance-inclined guys as C.A.G.R.

Let’s look at the pros and cons of this formula and see if it is a valuable tool to add to our arsenals as investors…

As usual:

A story of genius

A long time ago in a galaxy far, far away…

It’s 1916. In Petoskey, Michigan, a small rural town of less than 4,000 people, a little Claude Shannon is born.

Working at AT&T Bell Labs and later MIT, Shannon grew up to be one of the most influential minds of modern history. And I think it’s fairer to say “history” than “modern history”.

The list of contribution of this American genius is endless: from early genetics to the idea that computers should “do their things” using the now mainstream 0s and 1s, from helping defeat the Axis forces in WWII working on “Project X” together with Alan Turing (the Brit who cracked the nazis Enigma machine) to inventing the first wearable computer (precursor to the modern smart watches). But probably the most influential of Shannon’s works is a 1948 paper called “A Mathematical Theory of Communication”, in which he single-handedly invented Information Theory, a new science that studies the “quantification, storage, and communication of information”. This paper has been of the utmost importance for the success of space missions, the invention of the compact disc, mobile phones and the Internet, the study of linguistics, mathematics, statistics, computer science, physics, neurobiology… and much more but I think you got the point.

He retired early in his 40s, dedicating the rest of his life to personal interests such as artificial intelligence (A.I.) and the stock market.

From William Poundstone masterpiece, “Fortune’s Formula”:

There were many at Bell Labs and MIT who compared Shannon’s insight to Einstein’s. Others found that comparison unfair - unfair to Shannon.

It was actually a Bell Labs colleague of Shannon, John Kelly, who, in a 1956 paper called “A New Interpretation of Information Rate”, set out to find the answer to "the problem of “The gambler with a private wire” deriving the now famous Kelly Formula.

Consider a communication channel (private wire) which is used to transmit to a gambler the result of a horse race before the outcome becomes public knowledge. The gambler has therefore an advantage in the way that he can place bets at “markets” odds that are not adjusted for the private wire tips, and profit accordingly. The amount of money this gambler could make depends just on the amount wagered, given that he would win with absolute certainty.

The best strategy for long term wealth accumulation would be to bet 100% of the bankroll on each flip. He is sure to win.

Consider now another private wire with a “noisy” communication channel (a reference to Shannon’s Information Theory) in which these tips may not be 100% accurate. The old strategy of “bet it all” doesn’t work anymore, given that even a small chance of error in the private wire tips will result in the gambler going broke over a long enough period of time.

How much of his bankroll should our gambler wager each time?

This is the question answered in Kelly’s paper, with the equation (from Poundstone):

K = edge/odds

where K is the percentage of your bankroll to wager on a certain bet.

Goals and computation

As we’ve already seen, the goal of the Kelly Criterion is to “optimise (and maximise) for the geometric mean of returns, better known to finance-inclined guys as C.A.G.R”. That is, to maximize the expected value of the function “log(wealth)”.

Starting from edge/odds we can extrapolate a formula for investments:

for reference, here’s Thorp’s paper “The Kelly Criterion in Blackjack, Sports Betting, and the Stock Market”

Where:

• W = probability of positive outcome, in %

• B = % gain in the case of a positive outcome, calculated as: (positive outcome expected value - share price) / share price

• A = inverted % loss in the case of a negative outcome, calculated as: - (negative outcome expected value - share price) / share price

Let’s look at a theoretical example: a very dumb friend of yours offers to pay you $1.25 each time a coin flips on head. You have to pay him only $1 in the case of a tail. As we all know, the distribution of tail/head is 50/50. The Kelly Formula suggest us to bet 10% of our bankroll on each flip of a coin:

from the formula “W / A - (1 - W) / B = K”

0.5 [W] / 1 [A, -(0 - 1)/1] - (1 - 0.5) / 1.25 [B, (2.25 - 1)/1] = 0.10

Let’s compare the results of the Kelly Criterion with other popular money management systems over 250 of the bets described above:

• In blue, “Kelly”;

• In red, “Fixed wager [$0.05]” or betting $5 cents on each flip;

• In yellow, “Bet it all” or betting 100% of the bankroll on each flip;

• In green, “Martingale”.

As you can see in [Exhibit 1], the portfolio managed using the Kelly Criterion is the clear winner over the long run. That is because the Kelly Criterion is a proportionate betting system allowing the bettor to make optimal use of capital. Is it the only proportionate betting system? Not at all; one could decide to bet 1% or 99% or whatever percentage of its bankroll on each flip but the percentage computed by the Kelly Formula is the mathematical superior one, provided your goal is only to maximise terminal wealth in the long run:

X axis = % of bankroll on each flip; Y axis = x Multiple of original bankroll.

This simulation show us how, over a number n of bets, the optimal percentage of the total bankroll/portfolio to bet/invest is dictated by the Kelly Criterion, in this specific case 10.0%.

As demonstrated, the Kelly Criterion solves for one of the fundamental problems of investing and trading: position sizing.

Samuelsons v. Kelly

You’ve probably heard of Paul Samuelson. Together with Fama and French, Samuleson is credited, among many contributions to the field of economics, to have popularised the “Efficient Market Hypothesis” (EMH). He had such a strong belief in EMH that he bought stock in Buffet’s conglomerate Berkshire in the 70s, beating the market by a mile. Do as I do, not as I say.

This big shot economist was by far the most outspoken critique of the Kelly Criterion.

The first of Samuelson’s many arguments is relevant and worth of consideration.

While Samuelson acknowledged that “Acting to maximize the geometric mean [a.k.a CAGR] at every step will, if the period is sufficiently long, almost certainly result in higher terminal wealth […]”, he also acknowledged that, in his search for maximum wealth, the Kelly gambler is making certain trade-offs, specifically, he’s constantly risking a certain percentage of capital.

This argument is directly related to marginal utility, first introduce by Daniel Bernoulli in a 1738 paper called “Exploration of a New Theory on the Measurement of Risk”; marginal utility is the concept that different people, with different starting wealth levels, value the same income gain differently:

Not at scale

As shown in [Exhibit 3], the same increase in wealth (green horizontal line) results in higher utility (orange vertical line) for individual [A], worth $1,000, than for individual [B], worth $1,000,000.

The same way, it may be foolish, and actually it is foolish, for a 65 yrs. old on the verge of retiring to bet 10% of its wealth on a flip of a favorable coin as described above, even if this leads to suboptimal terminal wealth.

The Kelly Criterion should be used only if the goal is maximizing terminal wealth in the long run. Let me emphasize “terminal wealth” and “long run”.

But then, in the majority of cases, as told by Poundstone:

About the only rock-solid preference most people have about money is that they want as much of it as possible, as fast as possible.

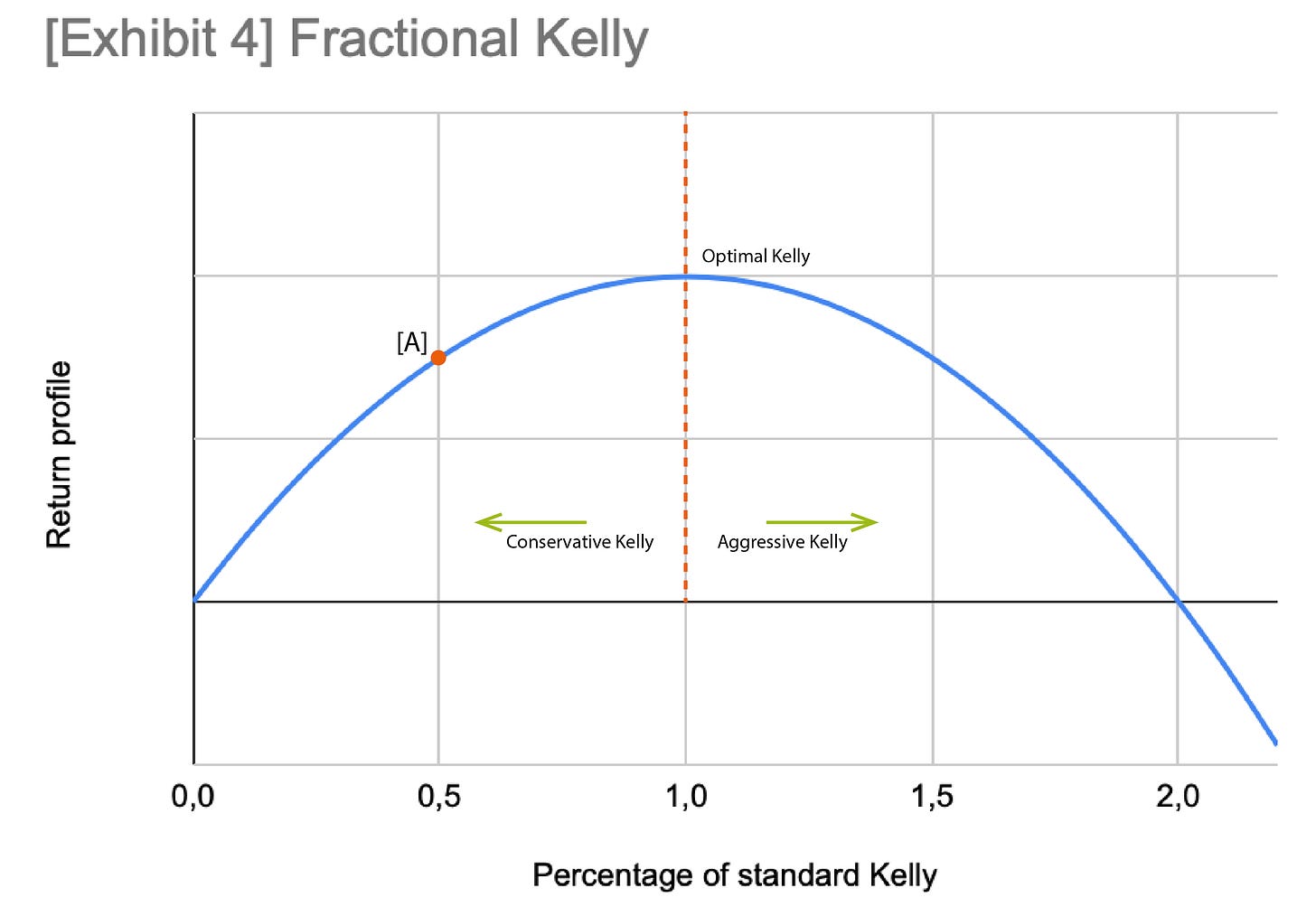
The second argument is related to the volatility of a portfolio managed with the Kelly Formula. While this certainly is true, as shown in [Exhibit 1], there are actually two methods to reduce volatility without sacrificing returns: [1] diversification and [2] fractional Kelly.

By placing a number of uncorrelated bets, allocating capital using the Kelly Criterion, it is possible to reduce volatility while increasing returns. A portfolio consisted of 10 of the coin flips aforementioned will fare much better than a portfolio of just 1 of the same coin flip. That is [1] diversification.

Another strategy is the use of [2] fractional Kelly instead of standard Kelly:

[Exhibit 4] (a generalization of [Exhibit 2]) shows the return profile of a generic investment or bet. Volatility increases from left to right.

Allocating capital following the standard Kelly Formula, 1.0, provides the best long term return, given that you can sustain volatility. Moving left to point [A], equal to half Kelly, or 0.5, volatility drastically decrease, by a factor of the square of two, while it doesn’t affect return all that much.

What I believe is that the number that comes out of the Kelly Criterion should be view as a hurdle, as the maximum number not to exceed, as the maximum position size not to exceed. That is because [1] any Kelly percentage higher than 1.0 increases volatility while reducing expected return, even going into negative expected return territory after double Kelly, and [2] to account for possible mistake in the inputs of the Kelly Criterion itself.

Let me add a consideration: in the end, a formula is just as good as its imputs. That is, if your calculations about probabilities and expected outcomes are wrong, the Kelly Criterion won’t provide any sort of guidance whatsoever.

A practical example

I think it is always useful to look at a practical example. I’ve chosen Clipper Realty [CLPR], you can find my full article here in case you’ve missed it.

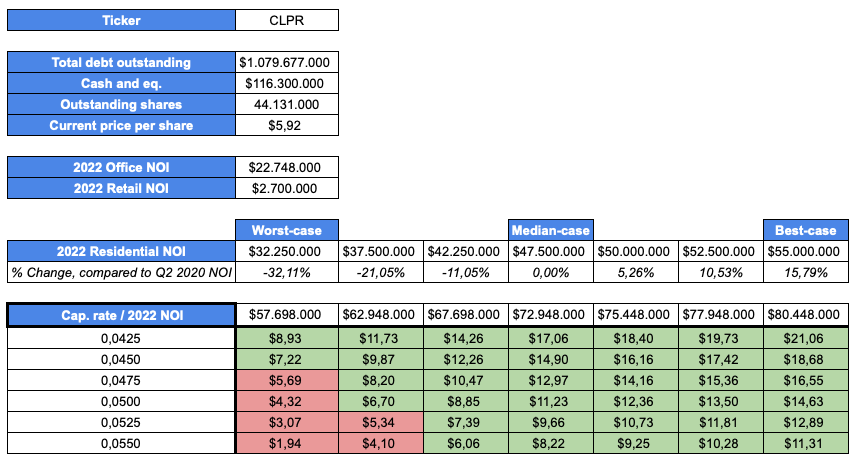
Let’s start from a valuation matrix:

taken from my write-up, updated to account for share price change, as of 10/27/2020

Green cells represent positive outcomes based on current share price of ~$5.90. red cells represent negative outcomes.

In my valuation I assumed an equal distribution of probabilities between different outcomes. I can compute the optimal allocation using the Kelly Criterion:

from the formula “W / A - (1 - W) / B = K”:

• W = 89.29%, positive outcomes probability (calculated as “n. of green cells divided by n. of total cells”)

• A = 30.85%, negative outcomes expected value (calculated as “- (red cells expected value - share price) / share price”

• B = 112.03%, positive outcomes expected value (calculated as “(green cells expected value - share price) / share price”

0.8929 / 0.3085 - (1 - 0.8929) / 1.1203 = 2.79

For a position in Clipper, based on my calculation, the optimal capital allocation is equal to 279% of the portfolio. I should lever up by almost a factor of 3 (!).

Let’s start by using a half-Kelly:

2.79 * 0.5 = 1.395 [half-Kelly]

139 percent, that’s still a big number.

Because the opportunities I’m looking for always present a risk-reward profile heavily skewed in my favour, I often ends up with suggested allocation in the 100s of percent. It’s not prudent to lever up my portfolio 10 to 1, even if it leads to suboptimal capital allocation. I’ve decided not to go on margin, therefore I’ve designed an easy method to reconcile the outputs from the various Kelly Formula calculations:

Using a basic proportion, by dividing the “Half Kelly” column by the sum (900.00% in this case), it is possible to reconcile the astronomical Kelly allocations. Let’s also say that you want at any moment a 20% cash allocation, you can multiply the “Standardised Kelly” by (1 - desired cash allocation):

Conclusions

You may be thinking “Ok, amazing. This works in theory. But has anyone ever benefited from it in the real world?”

A series of successful investors and money managers have used and use the Kelly Criterion for optimal capital allocation, among these Mohnish Pabrai and Claude Shanno (yes, the guy who started it all); the latter, after inventing a couple of new sciences, achieved a ~28% CAGR over 26 years (!).

John Kelly itself never used his formula to make money. The most vocal advocator for the Kelly Criterion is in fact Edward Thorp.

In the 1960s Thorp developed a card counting system, later published in “Beat the Dealer”, that tilted the odds of the game of Blackjack from the house to the player. He used the Kelly Criterion to constantly make money from casinos. He’s said to be making approximately $300,000 per year in the 60s.

But the most impressive of Thorp many endeavours is Princeton-Newport Partners, one of the first hedge funds in history, founded together with James Regan. The fund’s track record is impressive: from 1969 to 1988 the fund returned 15.1% per year (net of the typical 2/20 fees) compared to the S&P 8.8% per year. All of this with a standard deviation of just 4%, much lower than the index’s. After retiring from managing outside capital, the private partnership run by Thorp reportedly returned 20% per year over 28 years.

Jack Schwager, author of “Hedge Funds Market Wizards”, says this of Thorp:

He has, of all the traders I've ever interviewed, and in fact, of all the traders that ever existed, with the possible exception of Simons with Renaissance, and I'm not sure who has the better record, but he would, I'd think, have one of the two best records -- that has ever been compiled in trading -- in terms of return to risk.

Thorp itself attributes much of this risk-adjusted performance to the use of the Kelly Criterion.

I now want to bring to your attention another fund, a failure, where the use of Kelly could have helped: now infamous Long Term Capital Management (LTCM). The 1998 implosion of LTCM is one of the most impactful events in modern finance. The fund HAD to be bailed out by a consortium of Wall St. banks to avoid the collapse of the financial system.

One of the reasons behind this collapse, portrayed by Roger Lowenstein in his “When Genius Failed”, is overbetting. The long-term effects of overbetting are shown in [Exhibit 4].

This is the exact problem solved by Kelly in 1956: how much of his bankroll a gambler should wager on a bet to achieve the maximum terminal wealth while avoiding going under.

To close matters, here’s a thought-provoking quote on from Mauboussin:

As an investor, maximizing wealth over time requires you to do two things: find situations where you have an analytical edge; and allocate the appropriate amount of capital when you do have an edge. 

Thanks for reading.

Caveat emptor. Do not trust a 17 yrs. old on the internet. Do your own due diligence.

Bibliography and key sources

Fortune’s Formula, by William Poundstone (this is THE book, give it a read)

Patrick Boyle youtube channel

A New Interpretation of Information Rate, by John L. Kelly Jr.

Exploration of a New Theory on the Measurement of Risk, by Daniel Bernoulli

The Kelly Criterion in Blackjack, Sports Betting, and the Stock Market, by Ed. Thorp

Beat the Dealer, by Ed. Thorp

Beat the Market, by Ed. Thorp and Sheen T. Kassouf

A man for all markets, by Ed. Thorp

Size Matters, by Michael J. Mauboussin

The Kelly Criterion: You Don’t Know the Half of It, by Alan Bochman